Recherche linéaire
a- Comprendre
L'objectif est de savoir si une valeur est présente dans un tableau de données.
Peu importe les données (nombres, mots, ...) pourvu qu'elles soient déjà triées !
Le plus simple consiste à parcourir le tableau du début à la fin afin de savoir si la donnée recherchée est bien dedans.
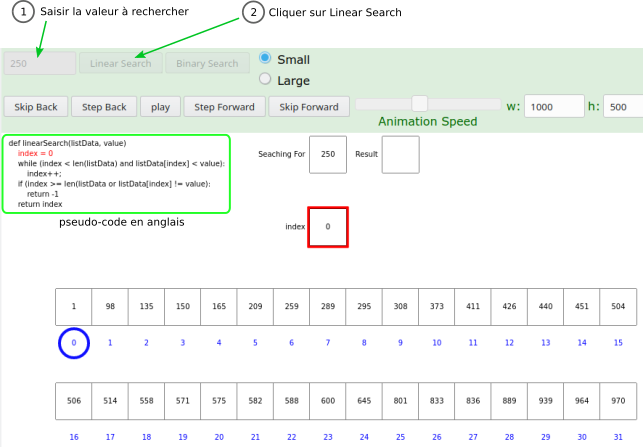
Une fois de plus, vous allez utiliser le site de l'université de San Fransico pour visualiser le fonctionnement de l'algorithme :
Attention : c'est du pseudo-code, ou algorithme qui est dans le rectangle vert et non du python, même si cela ressemble beaucoup. C'est normal, ce sont des anglais ! Vous aurez remarqué que le code est contenu dans une fonction.
Essayez plusieurs valeurs et observer pas à pas le fonctionnement du programme en cliquant sur Step Forward et non Play.
Je vous encourage aussi à lire et comprendre le paragraphe 2 du cours de Christophe DARMANGEAT afin de comprendre l'algorithme et la fameuse utilisation d'un Flag (drapeau).
b- Python
Faire un petit programme qui :
- initialise à tableau de 15 valeurs en respectant un tri croissant,
- définit la fonction de recherche linéaire rechLin(tab,val), - utiliser le pseudo-code donné sur le site de l'université de San Fransico comme base de départ.
- demande la valeur à trouver,
- appelle la fonction de recherche,
- qui affiche un message de valeur trouvée ou pas.
Vous testez votre programme bien évidemment avec au moins 2 jeux de test : si la valeur existe et si elle n'existe pas.
c- Complexité
La complexité est linéaire et d'ordre N puisqu'il faut parcourir dans le pire des cas toutes les valeurs du tableau et ce quelque soit la taille du tableau.
d- Conclusion
Cette technique n'est pas performante : car si la valeur recherchée se trouve vers la fin, il faut parcourir une grande part du tableau.
Voilà la raison d'être de la recherche dichotomique : gagner du temps !
a- Comprendre
Le principe de cet algorithme est de diviser en 2, le tableau de valeurs, et de déterminer si la valeur à recherche est avant ou après, puisque les valeurs dans le tableau sont triées ! Il suffit de recommencer ainsi de suite.
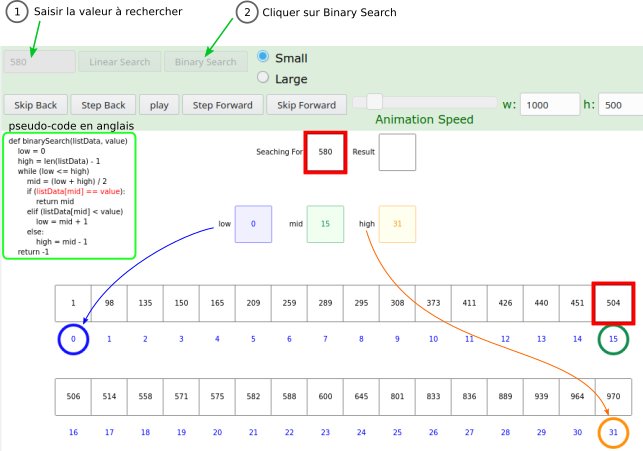
Le mieux est encore d'utiliser le site de l'université de San Fransico pour visualiser le fonctionnement mais en cliquant sur Binary Search qui est la traduction de Recherche dichotomique :
Essayez plusieurs valeurs et observer pas à pas le fonctionnement du programme en cliquant sur Step Forward et non Play.
Je vous encourage aussi à lire et comprendre le paragraphe 4 du cours de Christophe DARMANGEAT afin de comprendre l'algorithme et la fameuse utilisation d'un Flag (drapeau).
b- Python
Faire un petit programme qui :
- initialise à tableau de 16 valeurs en respectant un tri croissant,
- définit la fonction de recherche dichotomique rechDicho(tab,val), - utiliser encore une fois le pseudo-code donné sur le site de l'université de San Fransico comme base de départ.
- demande la valeur à trouver,
- appelle la fonction de recherche : exploiter l'algorithme de Christophe Darmangeat,
- qui affiche un message de valeur trouvée ou pas.
Vous testez votre programme bien évidemment avec au moins 2 jeux de test : si la valeur existe et si elle n'existe pas.
Compte tenu que l'on divise le tableau en deux, que se passe t-il si le nombre de valeurs du tableau est impair ?
N’hésitez pas à modifier votre tableau de départ avec 11 valeurs par exemple.
c- Complexité
La complexité est logarithmique.
Le tableau suivant compare les 2 algorithmes de recherche, pour le nombre de tours de boucle maximum (cas le plus défavorable de la position de la valeur à rechercher) :
| Taille du tableau | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | N |
| Recherche linéaire | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | N |
| Recherche dichotomique | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | log2 N |
Pour comprendre ce tableau concernant la recherche dichotomique, il faut se rappeler que l'objectif est de diviser par deux le tableau, puis de rediviser par deux jusqu'à arriver sur une seule valeur du tableau dans le pire des cas.
C'est exactement cela : 128/2=64, puis 64/2=32, puis 32/2=16, puis 16/2=8, puis 8/2=4, puis 4/2=2, puis 2/2=1 et enfin la dernière boucle pour comparer la dernière valeur et c'est fini. Cela fait bien 8 fois !
Qui se représente par le graphique suivant :
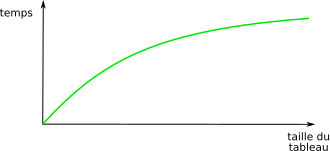
d- Conclusion
Entre les 2 techniques de recherche, la recherche dichotomique est la plus performante.
Par exemple, si l'on fait 1000 recherches dans une liste de 10millions de valeurs, la recherche linéaire prendra environ 20mn tandis que la recherche dichotomique ne mettra que 16ms pour y arriver, soit 75 000 fois plus rapide !
e- Exercice
Ecrire un programme qui exploite la recherche dichotomique afin de supprimer d'un tableau une valeur à rechercher (bien évidemment si elle existe).
Le programme aura la structure suivante :
- initialisation des valeurs d'un tableau de 12 éléments,
- définition de la fonction de recherche d'une valeur. Il sera judicieux que l'indice de la valeur trouvée soit aussi retournée.
- demander à l'utilisateur la valeur à rechercher,
- lancer la recherche avec la fonction
- à l'aide des paramètres retournée par la fonction, traiter les 2 cas de figure :
Si la valeur existe : supprimer l'élément du tableau. Cela signifie que le tableau ne contient plus que 11 éléments. Afficher un message comme quoi la valeur a été trouvée et supprimée du tableau.
Si la valeur n'existe pas : Afficher un message comme quoi la valeur n'a pas été trouvée.