Pourquoi cet algorithme ?

L'objectif est de résoudre un problème en optimisant la solution. On parle alors de problème d'optimisation.

C'est à dire que pour résoudre un problème, il existe souvent plusieurs solutions plus ou moins performantes.

Une méthode basique comme l'analyse combinatoire serait de trouver toutes les solutions possibles puis de les comparer pour trouver la meilleure.
C'est à dire qu'il faudrait rechercher toutes les combinaisons possibles pour trouver les solutions, puis de les comparer pour ne retenir que la meilleure.
On comprend aisément que la recherche de toutes les combinaisons possibles peut devenir très complexe en temps : de complexité exponentielle.

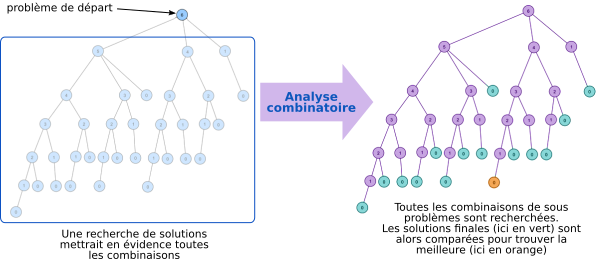
L'algorithme glouton ne va pas explorer toutes les possibilités, il va choisir des solutions locales optimales dans le but d'obtenir une solution idéale.

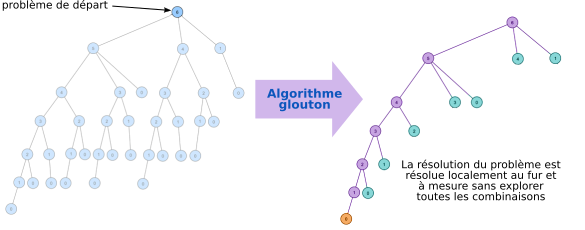
Les 2 figures ci-dessus montre que la solution idéale n'est pas identique : il arrive en effet que la solution trouvée par l'algorithme de glouton ne trouve pas la solution idéale.

Prenons l'exemple de la figure suivante :

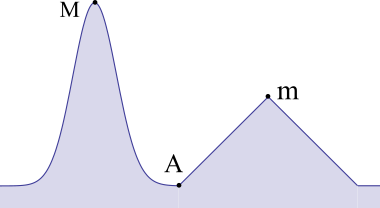
Imaginez que vous êtes au point A et que vous souhaitez monter sur le plus haut sommet et que vous voulez résoudre le choix de partir à gauche ou à droite avec un algorithme glouton.
Vous donnez comme critère de choix d'avoir la plus forte pente : au point A la plus forte pente est à droite et non à gauche. Vous n'attendrez pas le plus haut sommet.
Sur cet exemple visuel et extrêmement simple il est facile de répondre sans algorithme.

Vous comprenez que la manière de poser le problème est essentiel et qu'il arrivera à l'algorithme glouton de trouver une bonne solution, mais pas la meilleure. Et il ne sera pas facile de déterminer sur des problèmes complexes si la solution proposée sera la meilleure.

Passons à la pratique

Vous allez faire les activités du cambrioleur et du rendu de monnaie sur le site  Pixees

Une correction possible est la suivante

#déclaration des variables
MonaieEurope=[1,2,5,10,20,50,100,200,500]
SommeARendre=463
#fonction méthode glouton - recherche solution locale
# S : liste des billets, monaies du système européen
def gloutonMonaie(S,X):
    nb = 0
    while X>0:
        nb+=1                            #écriture identique à nb=nb+1
        i = 0
        while (i<len(S)) and (S[i]<=X):
            i+=1
        MonaieARendre[i-1]=MonaieARendre[i-1]+1
        X-=S[i-1]                        #écriture identique à X=X-S[i-1]
    return nb
#initialisation tableau MonaieARendre
def InitMonaieARendre(S):
    M=[]
    i=0
    while (i<len(S)):
        M.append(0)
        i+=1
    return M
#Recherche et affichage des solutions
MonaieARendre=InitMonaieARendre(MonaieEurope)
nbResol=gloutonMonaie(MonaieEurope,SommeARendre)
print("Les pièces à rendre sont",MonaieARendre)
print("Le problème a été résolu en",nbResol,"sous problèmes")

Vous devez obtenir

Les pièces à rendre sont [1, 1, 0, 1, 0, 1, 0, 2, 0]
Le problème a été résolu en 6 sous problèmes

Le schéma suivant montre les différentes étapes de résolution du problème :

Changer la valeur de SommeARendre afin de vérifier le bon fonctionnement de l'algorithme.

Modifier le programme concernant l'affichage des résultats, de telle sorte qu'on obtienne une présentation comme :

Les pièces à rendre sont :
2 pièce(s) de 200
1 pièce(s) de 50
1 pièce(s) de 10
1 pièce(s) de 2
1 pièce(s) de 1